von
Dr. Roland Mildner, Leipzig (home)
Im Folgenden möchte ich Ihnen die "Trio-Würfel" vorstellen, ein interessantes logisches
Spielzeug für Jedermann, das ich mir im Jahre 1987 ausgedacht und im Heft 5 / 1988 der
damaligen mathematischen Schülerzeitschrift "alpha" veröffentlicht habe.
Es handelt sich bei den Trio-Würfeln um einen logischen Würfel-Baukasten, bestehend aus
27 gleich großen Teilwürfeln, die mit 3 Farben (Blau, Gelb, Rot) so gefärbt sind, dass mit
ihnen der Zusammenbau eines 3 x 3 x 3 - Würfels mit einfarbiger Oberfläche möglich ist,
wobei aber jede der drei Farben die Oberflächenfarbe sein kann. Das Auffinden der dazu
erforderlichen Färbung der 27 Würfel war dabei das eigentliche mathematische Problem (s.
Mathematik der Trio-Würfel ).
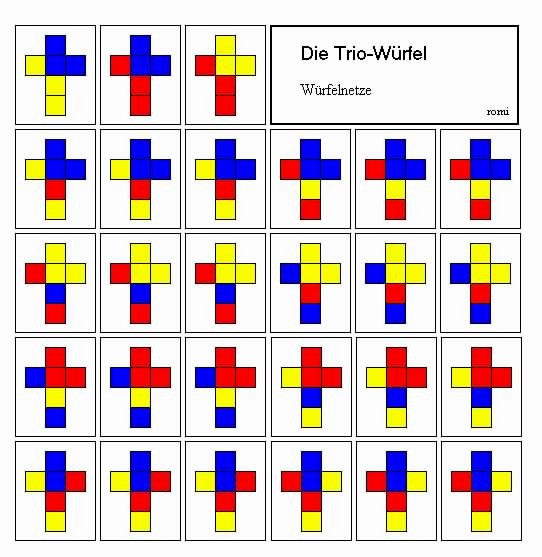
Die folgende Abbildung zeigt die Netze der Trio-Würfel,
die man durch Farbanstrich bzw. Bekleben mit Buntpapier selbst herstellen kann (s. auch
Herstellungsanleitung für die Trio-Würfel).
Die Trio-Würfel gestatten eine Reihe von
Baumöglichkeiten mit unterschiedlichem logischen Schwierigkeitsgrad
(s.Spielmöglichkeiten
mit den Trio-Würfeln und
Weitere Aufgaben und Probleme ). Im Gegensatz zum bekannten
6-farbigen ungarischen Rubik-Würfel, dessen Beherrschung nur wenigen "Spezialisten"
vergönnt ist, sind die Trio-Würfel für Jedermann, insbesondere auch für Kinder, geeignet.
Doch leider wurden die Trio-Würfel bisher noch nicht industriell gefertigt und vermarktet.
Vielleicht findet sich auf diesem Wege ein Hersteller
(s.Vorschläge zur industriellen Fertigung
der Trio-Würfel ).
1. Herstellungsanleitung für die Trio-Würfel ( zum Anfang )
Hat man 27 gleich große Würfel zur Hand, so kann man sich die Trio-Würfel durch
Farbanstrich bzw. Bekleben mit Buntpapier selbst herzustellen. Das ist nach den in der
obigen Abbildung dargestellten Würfelnetzen möglich; man könnte aber auch systematisch
nach einer der folgenden beiden Färbungsvorschriften vorgehen:
Färbungsvorschrift 1:
Man stelle 27 gleich große Würfel in fünf Reihen zu je 3, 6, 6, 6 und 6 Würfeln wie in der
Abbildung "Würfelnetze" auf und färbe sie wie folgt ( D = Deckfläche, G = Grundfläche,
V = Vorderfläche, R = Rückfläche, LS = linke Seitenfläche, RS = rechte Seitenfläche):
1. Reihe (bestehend aus 3 Würfeln): V, D und RS werden beim linken und mittleren Würfel
blau, beim rechten Würfel gelb gefärbt. Die drei Restflächen werden beim linken Würfel
gelb sowie beim mittleren und rechten Würfel rot gefärbt.
2. Reihe (3. Reihe, 4. Reihe): V, D und RS aller 6 Würfel werden blau (gelb, rot) gefärbt.
Man bildet nun zwei Gruppen zu je 3 Würfeln. Bei der linken Gruppe werden R und LS
gelb (rot, blau) und G rot (blau, gelb), bei der rechten Gruppe R und LS rot (blau, gelb)
und G gelb (rot, blau) gefärbt.
5. Reihe: V und D aller 6 Würfel werden blau gefärbt. Dann bildet man wieder zwei
Gruppen zu je 3 Würfeln. Bei der linken Gruppe werden R und LS gelb sowie G und RS
rot, bei der rechten Gruppe R und RS gelb sowie G und LS rot gefärbt.
Färbungsvorschrift 2:( Zurück zu Lösung 2
/ Zurück zu Abschnitt 4 )
Man setze 27 gleich große Würfel zu einem 3 x 3 x 3 - Würfel zusammen und färbe dessen
Oberfläche mit der ersten Farbe (etwa Blau). Dann ziehe man die 3 Schichten von je 9
Würfeln in jeder der drei räumlichen Richtungen (links-rechts, vorn-hinten, oben-unten)
auseinander und färbe in jedem Falle zwei gegenüberliegende Schichtflächen mit der
zweiten Farbe (etwa Gelb) und die beiden anderen gegenüberliegenden Schichtflächen mit
der dritten Farbe (etwa Rot) so, dass der Zentralwürfel zwei einfarbige Ecken (1 gelbe
und 1 rote) hat.
2. Spielmöglichkeiten mit den Trio-Würfeln ( zum Anfang )
Mit den Trio-Würfeln können ein-, zwei- und dreifarbige Körper gebaut werden (s.dazu die
Abbildungen Einige Würfelmodelle und Einige Häusermodelle). Dabei besteht der Reiz bzw.
die Schwierigkeit beim Zusammenbau der Würfel bzw. Gebäudemodelle darin, dass man
mit den zur Verfügung stehenden Würfel-Farbflächen haushalten muss. Baut man etwa beim
Zusammenfügen eines einfarbigen blauen 3 x 3 x 3 - Würfels eine blaue Fläche ins Innere
ein, so fehlt diese am Schluss. Der Fehler ist aber durch Austausch des fälschlich eingebauten
Würfels leicht korrigierbar. Man erkennt den logischen Reiz beim Spiel mit den Trio-Würfeln
am besten, indem man erst einmal die drei einfarbigen Würfelmodelle (Würfel Nr. 1,2 oder 3
in der Abb. "Einige Würfelmodelle") zusammenbaut. Dabei muss man sich schon überlegen,
welche Würfel als Eckwürfel, Kantenwürfel, Flächenwürfel bzw. als Zentralwürfel fungieren
können. Und erst dann sollte man versuchen, die anderen in den folgenden Abbildungen
dargestellten Würfel- und Gebäudemodelle zu bauen. Die Trio-Würfeln bieten für jede
Altersgruppe und jeden Intellekt einen angepassten Schwierigkeitsgrad. Insbesondere
können durch das Spiel mit den Trio-Würfeln bei Kindern räumliches Vorstellungsvermögen,
Farbempfinden, Phantasie und logisches Denken entwickelt werden. Aber selbst erfahrenen
Knoblern und sogar Mathematikern bieten die Trio-Würfel harte Nüsse zum Knacken. Ich
denke hier etwa an Modelle mit inneren Anschlussbedingungen, denn der Bau eines Modells
wird wesentlich schwieriger, wenn man fordert, dass etwa die "einfache Anschlussbedingung"
(je zwei im Inneren aufeinander liegende Würfelflächen haben gleiche Farbe) bzw. sogar die
"verschärfte Anschlussbedingung" (aufeinander liegende Schichtflächen des Modells sind
gleich farbig) erfüllt sein sollen. Schwierig kann auch die Beantwortung der Frage sein, welche
farblichen Modelle überhaupt mit den Trio-Würfeln gebaut werden können und welche nicht.
Versuchen Sie nun einmal, die in den folgenden Abbildungen dargestellten Würfelmodelle und
Häusermodelle zusammenzubauen. Beginnen Sie dabei, wie oben bereits erwähnt, mit dem
Zusammenbau der Würfelmodelle Nr.1, 2 und 3. Es ist ratsam, sich bei einer "Bau-Sitzung"
nur wenige Modelle vorzunehmen, diese aber um so genauer in Bezug auf ihre Bau-Logik zu
betrachten. Und erst nach genügend "Bau-Erfahrung" sollte man versuchen, die sich unten
anschließenden Aufgaben zu lösen.
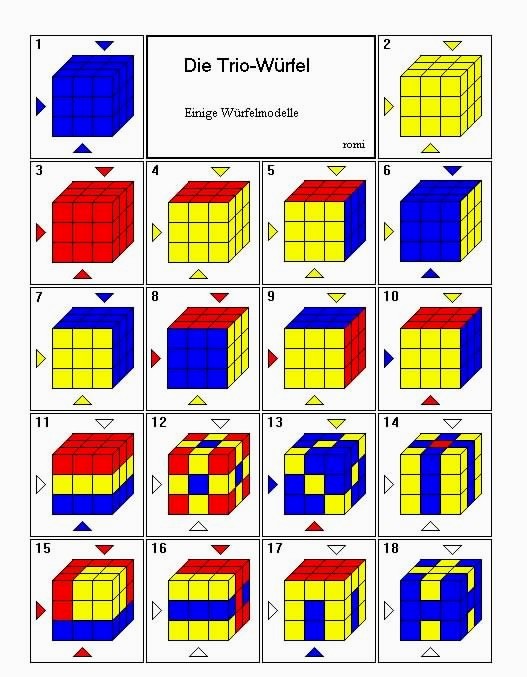
In den folgenden Abbildungen bedeutet ein farbiger Pfeil nach rechts (oben, unten), dass
die linke Seitenfläche (Grundfläche, Rückfläche) die Pfeilfarbe haben soll. Ein weißer Pfeil
bedeutet, dass die dadurch bezeichnete Fläche dieselbe Farbgebung wie die ihr gegenüber
liegende Fläche hat.
Und nun viel Spaß beim Zusammenbau der folgenden Würfelmodelle !
( Zurück zu Abschnitt 2
/ Zurück zu Abschnitt 4 )
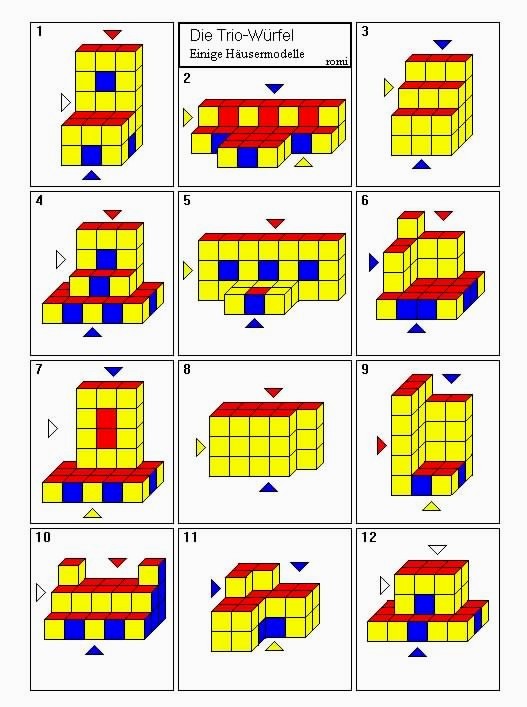
Und nun viel Spaß beim Zusammenbau der folgenden Häusermodelle !
( Zurück zu Abschnitt 2
/ Zurück zu Abschnitt 4 )
( Zurück zu Abschnitt 2
/ Zurück zu Abschnitt 4 )
Weitere Aufgaben und Probleme: ( zum Anfang )
1. Bauen Sie einen einfarbigen (etwa blauen) Würfel, der die einfache Anschlussbedingung
erfüllt ! ( Lösung 1 )
2. Bauen Sie einen einfarbigen (etwa gelben) Würfel, der die verschärfte Anschlussbedingung
erfüllt ! Welcher Zusammenhang besteht mit der obigen "Färbungsvorschrift 2" ?
( Lösung 2 )
3. Man greife unterschiedliche Trio-Würfel heraus und baue sie vergrößert im Format
2 x 2 x 2 bzw. 3 x 3 x 3 nach ! ( Lösung 3 )
4. Man überlege sich, ob mit den Trio-Würfeln gleichzeitig ein blauer, ein gelber und ein roter
2 x 2 x 2 - Würfel gebaut werden kann ! ( Lösung 4 )
5. Geben Sie Beispiele für farbige Gebäudemodelle an, die mit den Trio-Würfeln nicht gebaut
werden können! ( Lösung 5 )
3. Mathematik der Trio-Würfel ( zum Anfang )
Ausgangspunkt für die Färbung der 27 Trio-Würfel war das folgende Färbungsproblem:
Kann man einen Würfelsatz, bestehend aus 27 gleich großen Würfeln, mit drei
verschiedenen Farben so färben, dass mit ihm der Zusammenbau eines
3 x 3 x 3 - Würfels mit einfarbiger Oberfläche möglich ist, wobei jede der drei
Farben die Oberflächenfarbe sein kann ?
Wenn ja, so sind alle derartigen Färbungen, die wir "zulässige Färbungen" nennen wollen,
anzugeben. Dabei sollen die Färbungen von zwei Würfelsätzen als "gleich" angesehen
werden, wenn man die Würfelsätze, betrachtet als Würfelmengen, eineindeutig so aufeinander
abbilden kann, dass je zwei dabei einander zugeordnete Würfel die gleiche Färbung besitzen
(bis auf Würfeldrehung). Wir wollen zur Färbung o.B.d.A. die drei Farben Blau, Gelb und
Rot wählen.
Analyse des Problems:
Nehmen wir an, unser aus 27 Würfeln bestehender Würfelsatz sei bereits zulässig gefärbt,
und ein z.B. roter 3 x 3 x 3 - Würfel sei daraus gebaut. Dann müssen offenbar 8 Würfel (die
Eckwürfel) je drei eine Ecke bildende rote Flächen, 12 Würfel (die Kantenwürfel) je zwei in
einer Kante zusammenstoßende rote Flächen und 6 Würfel (die Flächenwürfel) je eine rote
Fläche tragen. Es müssen also 54 rote Flächen auf 26 Würfeln nach obiger Anordnung liegen.
Die innen liegenden 108 Flächen und somit der nicht sichtbare 27. Würfel (der Zentralwürfel)
müssen folglich nur die beiden anderen Farben Blau und Gelb tragen, denn für den Bau des
blauen bzw. gelben 3 x 3 x 3 - Würfels benötigt man ja ebenfalls je 54 blaue bzw. 54 gelbe
Flächen. Daraus ergibt sich, dass ein zulässig gefärbter Würfelsatz genau drei Würfel, die
jeweils als Zentralwürfel fungieren, enthalten muss, die nur zwei Farben (in gegenseitiger
Kombination auf je drei Eckflächen) tragen. Und die anderen 24 Würfel müssen alle drei
Farben tragen, wobei 6 Würfel je drei blaue Eckflächen, 6 Würfel je drei gelbe Eckflächen,
6 Würfel je drei rote Eckflächen (jeweils zusammen mit zwei Flächen mit gemeinsamer Kante
der zweiten Farbe und einer Fläche der dritten Farbe) und 6 Würfel die 3 Farben auf je zwei
Flächen mit gemeinsamer Kante tragen müssen.
Lösung des Problems:
Beschreiben wir jeden Würfel unseres Würfelsatzes durch ein geordnetes Farbtripel (b, g, r),
wobei b die Anzahl seiner blauen, g seiner gelben und r seiner roten Flächen angibt ( b, g, r
ganzzahlig; 0 [ b, g, r [ 6; b + g + r = 6 )
, so muss nach obigen Überlegungen ein zulässig
gefärbter Würfelsatz (zunächst noch ohne Berücksichtigung der geometrischen Anordnung
der Farben auf einem solchen Würfel) enthalten:
(1) - die 3 Würfel (3, 3, 0), (3, 0, 3) und (0, 3, 3),
(2) - 6 Würfel vom Typ (2, 2, 2),
(3) - x1 Würfel vom Typ (3, 2, 1) und x2 Würfel vom Typ (3, 1, 2) mit x1 + x2 = 6,
(4) - x3 Würfel vom Typ (1, 3, 2) und x4 Würfel vom Typ (2, 3, 1) mit x3 + x4 = 6,
(5) - x5 Würfel vom Typ (2, 1, 3) und x6 Würfel vom Typ (1, 2, 3) mit x5 + x6 = 6.
Da die 18 Würfel (3), (4) und (5) offenbar noch 36 Flächen von jeder Farbe tragen müssen,
so liefert das (diophantische) lineare Gleichungssystem
| (6) |
3 x1 + 3 x2 + x3 + 2 x4 + 2 x5 + x6 = 36 2 x1 + x2 + 3 x3 + 3 x4 + x5 + 2 x6 = 36 x1 + 2 x2 + 2 x3 + x4 + 3 x5 + 3 x6 = 36 x1 + x2 = 6 x3 + x4 = 6 x5 + x6 = 6 |
| (7) | xi ganzzahlig, 0 [ xi [ 6 ( i = 1, 2, 3, 4, 5, 6 ), |
nach dem Gaußschen Algorithmus und unter Beachtung von (7) erhält man die folgenden
sieben Lösungs-6-tupel (x1 , x2 , x3 , x4 , x5 , x6 ):
| (8) |
(6, 0, 6, 0, 6, 0), (5, 1, 5, 1, 5, 1), (4, 2, 4, 2, 4, 2), (3, 3, 3, 3, 3, 3), (2, 4, 2, 4, 2, 4), (1, 5, 1, 5, 1, 5), (0, 6, 0, 6, 0, 6), |
Berücksichtigt man jetzt noch die geometrische Anordnung der Farben auf einem Würfel, so
zeigt sich, dass zwar bei jedem der 21 Würfel (1), (3), (4) und (5) durch das Farbtripel und
die Eckbildungsvorschrift die Farbanordnung (bis auf Würfeldrehung) eindeutig festgelegt ist,
dass aber die 6 Würfel (2) zwei geometrisch verschiedene Farbanordnungen, die nicht durch
Würfeldrehung ineinander übergeführt werden können, zulassen. Denn hat man eine Farbe
auf zwei in einer Kante zusammenstoßenden Flächen aufgetragen, so gibt es für die zweite
Farbe zwei mögliche Anordnungen, nämlich linksherum (FL) bzw. rechtsherum (FR); die
Lage der restlichen zwei Flächen mit der dritten Farbe steht dann fest.
Bei jeder der sieben obigen durch (8) charakterisierten zulässigen Färbungen (ohne eine
Berücksichtigung der geometrischen Anordnung) hat man also sieben Möglichkeiten für die
Wahl der sechs Würfel (2), nämlich keinen Würfel mit (FL) und 6 Würfel mit (FR), 1 Würfel
mit (FL) und 5 Würfel mit (FR), usw., wobei die Farbgebung
| (9) | 3 Würfel mit (FL) und 3 Würfel mit (FR) |
zulässige Färbungen unseres Würfelsatzes. Unter diesen 49 zulässigen Färbungen gibt es nun
genau eine Färbung, nämlich die durch (1), (2) mit (9) sowie (3), (4) und (5) mit (8)
bestimmte, die durch eine beliebige Permutation der drei Farben nicht verändert wird. Diese
symmetrische Färbung wurde nun für die Trio-Würfel gewählt, die damit enthalten:
| (10) |
1 Würfel vom Typ (3, 3, 0), 1 Würfel vom Typ (3, 0, 3), 1 Würfel vom Typ (0, 3, 3), 3 Würfel vom Typ (3, 2, 1), 3 Würfel vom Typ (3, 1, 2), 3 Würfel vom Typ (1, 3, 2), 3 Würfel vom Typ (2, 3, 1), 3 Würfel vom Typ (2, 1, 3), 3 Würfel vom Typ (1, 2, 3), 3 Würfel vom Typ (2, 2, 2) nach (FL), 3 Würfel vom Typ (2, 2, 2) nach (FR), | ( Zurück zu Abschnitt 4 ) |
Kante gemeinsam haben müssen. Da die Färbung (10) der Trio-Würfel eine symmetrische ist,
d.h. dass eine beliebige Permutation der drei Farben die Färbung des Bausatzes insgesamt
nicht verändert, so ist also jedes gebaute Würfel- oder Gebäudemodell nur ein Vertreter einer
Klasse von Modellen, die sich lediglich durch Permutation der Farben unterscheiden.
4. Vorschläge zur industriellen Fertigung der Trio-Würfel ( zum Anfang )
Obwohl ich "Die Trio-Würfel" bereits im Heft 5 / 1988 der damaligen mathematischen
Schülerzeitschrift "alpha" veröffentlicht habe und somit in mancher deutschen Wohnstube
und in manchem schulischen Mathe-Zirkel (nach Selbstherstellung der Würfel) schon damit
gespielt wird, so wäre es doch schade, wenn die Trio-Würfel nicht industriell gefertigt und
weltweit vertrieben würden. Denn ich kann mir vorstellen, dass die Trio-Würfel ein Hit auf
dem deutschen und auch internationalen Markt werden könnten. Denn im Gegensatz zu dem
weltberühmten sechsfarbigen ungarischen Rubik-Würfel, dessen Teilwürfel drehbar fest
zusammengefügt sind und dessen Beherrschung nur wenigen "Spezialisten" vergönnt war und
ist, sind die Trio-Würfel nicht fest verbunden, damit leicht austauschbar, und Fehler beim
Zusammenbau sind leicht korrigierbar. Somit sind die Trio-Würfel für Jedermann geeignet.
Besonders wertvoll sind sie für Kinder, da durch das Spielen mit den Trio-Würfeln räumliches
Vorstellungsvermögen, Farbempfinden, Phantasie und logisches Denkvermögen spielerisch
entwickelt werden. Doch selbst erfahrenen Knoblern und sogar Mathematikern bieten die
Trio-Würfel harte Nüsse zum Knacken.
Die Technologie zur Herstellung der Trio-Würfel, die sicherlich nicht ganz einfach ist, könnte
sich an den obigen Färbungsvorschriften ( Färbungsvorschrift 1 oder 2 ) orientieren. Günstiger
aber wird es sein, jeden der 11 Würfeltypen
( vgl.(10) ) getrennt und en masse herzustellen,
um hiervon dann die notwendigen 27 Würfel für jedes Trio-Würfel-Spiel auszusortieren.
Zum Verkauf sollten die 27 Trio-Würfel in einem durchsichtigen und würfelförmigen Gefäß
untergebracht werden, wobei die Würfel der optischen Anziehungskraft wegen etwa wie im
Würfelmodell Nr. 12 einsortiert werden könnten. Natürlich müsste eine kurze Anleitung mit
den Abbildungen "
Einige Würfelmodelle " und " Einige Häusermodelle " beigefügt werden.
Ich stelle mir vor, dass man die Trio-Würfel in drei verschiedenen Ausführungen produzieren
könnte:
1. Eine kleine Ausführung für Reise und Urlaub (Kantenlänge eines Teilwürfels etwa 2 cm);
2. Eine Tischausführung für zu Hause oder für Kindereinrichtungen (Kantenlänge eines
Teilwürfels etwa 5 cm);
3. Eine aus großen Plaste-Hohlwürfeln gefertigte Ausführung insbesondere für
Kindereinrichtungen (Kantenlänge eines Teilwürfels etwa 30 bis 40 cm). Mit diesen leichten
und großen Farb-Würfeln könnten die Kinder dann Häusermodelle in ihrer Körpergröße
bauen (etwa gelbe Gebäude mit roten Dächern und blauen Fenstern), wobei räumliches
Vorstellungsvermögen, Farbempfinden, Phantasie und logisches Denkvermögen spielerisch
entwickelt werden.
Sollte sich ein Spiele-Produzent für die Trio-Würfel interessieren, so würde ich mich über eine
eMail seinerseits sehr freuen und sofort reagieren.
5. Lösungen zu "Weitere Aufgaben und Probleme"
Lösung 1: Die folgende Abbildung zeigt ein mögliches Modell eines einfarbigen blauen
Würfels, der nur die einfache Anschlußbedingung erfüllt:
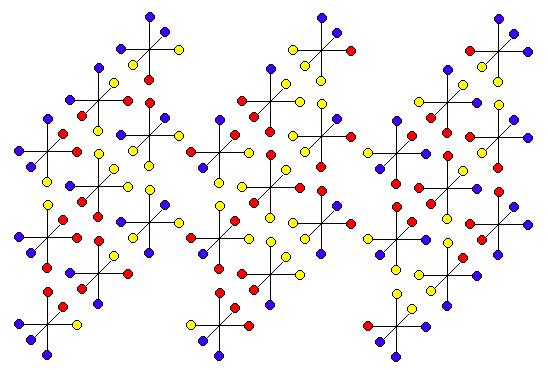
Lösung 2: Die folgende Abbildung zeigt ein mögliches Modell eines einfarbigen gelben
Würfels, der die verschärfte Anschlußbedingung erfüllt. Dieses Würfelmodell entspricht dem
Vorgehen bei der Färbungsvorschrift 2, wobei hier als 1. Farbe Gelb genommen wurde.
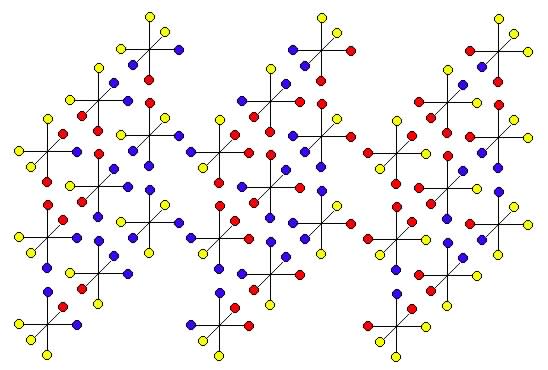
Lösung 3: Mit den Trio-Würfeln ist es möglich, alle diese Würfel zu bauen. Viel Spaß dabei!
Lösung 4: Es ist nicht möglich, mit den Trio-Würfeln parallel zueinander einen blauen, einen
gelben und einen roten 2 x 2 x 2 - Würfel zu bauen, denn in den erstgebauten einfarbigen
Würfel müssen bereits zwei einfarbige Würfelecken mit den beiden anderen Farben eingebaut
werden, die dann für den Bau des zweiten oder dritten Würfels fehlen.
Lösung 5: Wegen der Spezifik der Färbung der Trio-Würfel (3 der 27 Trio-Würfel tragen
nur 2 Farben, gegenüberliegende Würfelflächen sind niemals gleich farbig, begrenzte Anzahl
von Würfeln eines bestimmten Typs) können z.B. nicht gebaut werden:
a) aus den 27 Würfeln bestehende nichtwürfelförmige Modelle mit einfarbiger Oberfläche,
b) aus den 27 Würfeln bestehende Mauern (Dicke: 1 Würfelseite) mit einer einfarbigen
Wandfläche.
c) Gebäudeteile (Dicke: 1 Würfelseite) , bei denen gegenüberliegende Teilflächen gleich
farbig sind.