von Dr. Roland Mildner (Leipzig 2001)
Am 12.April 2002 jährt sich zum 150. Mal der Geburtstag des deutschen Mathematikers Carl Louis Ferdinand von Lindemann (1852 - 1939). Seine bedeutendste mathematische Leistung war der Beweis, dass die Kreiszahl π eine transzendente Zahl ist. Damit hatte er das jahrtausendealte Problem der Quadratur des Kreises mit Zirkel und Lineal gelöst, d. h. er hatte streng mathematisch bewiesen, dass es nicht möglich ist, einen Kreis allein mit Zirkel und Lineal in ein flächengleiches Quadrat zu verwandeln. Diese wissenschaftliche Leistung bezeichnete der Mathematiker Constantin Carathéodory (1873 - 1950) in einem Nachruf auf Lindemann als "einen Glanzpunkt in den mathematischen Erfolgen der Neuzeit".
Carl Louis Ferdinand von Lindemann wurde am 12.4.1852 in Hannover geboren. Von 1870
bis 1873 studierte er an mehreren Universitäten, so in Göttingen, Erlangen, München,
Paris und London. Im Jahre 1873 promovierte er zum Dr. phil. bei dem Mathematiker Felix Klein (1849 - 1925) in Erlangen. 1877 wurde er Privatdozent in
Würzburg und im gleichen Jahr außerordentlicher und 1879 ordentlicher Professor für Mathematik an der Universität Freiburg
(i. Breisgau). Von 1883 bis 1893 war Lindemann Professor an der Universität Königsberg
(Kaliningrad). 1893 folgte er einem Ruf an die Universität München, wo er bis zu seiner Emeritierung im Jahre 1923 als Professor für Mathematik tätig
war. Lindemann wurde 1895 ordentliches Mitglied der Bayerischen Akademie der Wissenschaften zu München, und er
war Ehrenmitglied der Universität Würzburg. Er starb am 6.3.1939 in München.
Ferdinand von Lindemann war ein vielseitiger Mathematiker und wissenschaftlich sehr produktiv.
Er beschäftigte sich mit vielen Gebieten der reinen Mathematik, aber besonders intensiv mit Zahlentheorie, Differentialgeometrie und algebraischer Geometrie,
und seine Arbeiten dazu sind reich an wichtigen Erkenntnissen und Ergebnissen. Darüber hinaus schrieb er
aber auch einige wissenschaftliche Arbeiten über Mechanik, Astronomie, Molekularphysik, Spektraltheorie und Geschichte der Mathematik.
Die bedeutendste Leistung Lindemanns jedoch war sein Beweis der Transzendenz der Kreiszahl π .
Die Zahl π ist eine der wichtigsten und interessantesten mathematischen Konstanten. Sie ist geometrisch als Verhältnis des Umfanges u eines Kreises zu
seinem Durchmesser d = 2r bestimmt, also u / d = π .
Die Zahl π gibt aber auch das Verhältnis des Flächeninhalts A eines Kreises zum Quadrat über seinem Radius r an, also A / r2 = π .
Für r = 1 (LE) ergibt sich
A = π (LE)2, also stellt π auch den Flächeninhalt des Einheitskreises dar. Und wegen dieser geometrischen Deutungen wird π wohl gern als "Kreiszahl" bezeichnet.
Doch welchen zahlenmäßigen Wert und welche Eigenschaften hat die Zahl &pi ? Es bedurfte eines langen historischen Prozesses, um die Antwort auf diese Fragen zu erbringen:
Zahlenmäßig war die Zahl &pi schon mit unterschiedlicher Genauigkeit den Kulturvölkern des Altertums
bekannt. So kannten die alten Ägypter im 17. Jahrhundert v. u. Z. für π schon den Näherungswert
(16 / 9)2 ≈ 3,16. Der griechische Gelehrte Archimedes von Syrakus (um 287 v. u. Z. - 212 v. u. Z.) bestimmte brauchbare Näherungswerte
für &pi durch die Berechnung des Umfanges von n-Ecken, die einem Kreis ein- bzw. umbeschrieben sind.
Für n = 96 erhielt er die Abschätzung 223 / 71 < π < 22 / 7. Daher rechnet man oft auch grob mit π ≈ 22 / 7.
Der französische Mathematiker Francois Vieta (1540 - 1603) führte dieses Archimedische Verfahren bis zum 6 ⋅ 216-Eck,
also dem 393216 - Eck fort und bestimmte die Zahl π auf 9 Dezimalstellen genau, er fand nämlich:
3, 141 592 653 5 < π < 3,141 592 653 7. Auch der
holländische Gelehrte Ludolf van Ceulen (1540 - 1610) benutzte das Verfahren von Archimedes und berechnete &pi bis auf 35 Dezimalen genau.
Nach ihm wird π auch als "Ludolfsche Zahl" bezeichnet.
Ohne die folgenden Begriffe im Rahmen dieses Artikels genauer erläutern zu können, sei bemerkt,
dass im 17. und 18. Jahrhundert die Zahl π vor allem durch unendliche Reihen (1), unendliche Produkte (2) und unendliche Kettenbrüche (3) dargestellt und
näherungsweise berechnet wurde, z.B.
nach Gottfried Wilhelm Leibniz (1646 - 1716):
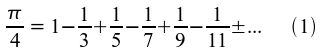
nach John Wallis (1616 - 1703):
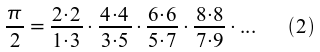
nach Lord William Brouncker (1620 - 1684):
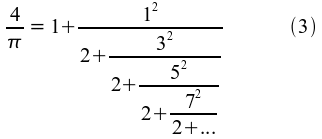
Bemerkt sei, dass sich die Reihe (1) aus der von James Gregory (1637 -1675) gefundenen Arkustangensreihe
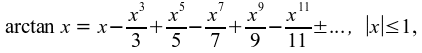
Das Symbol π (= erster Buchstabe des griechischen Wortes περιφερεια für "Kreislinie") wurde allerdings erstmals im Jahre 1706 von William Jones (1675 - 1749) in seiner Arbeit "Synopsis palmariorum matheseos or new introduction to the mathematics" (London 1706, S.243) benutzt. Allgemeine Verbreitung fand die Bezeichnung π für die Kreiszahl aber erst durch Leonhard Euler, der in früheren Arbeiten anstelle des π das p (= erster Buchstabe des lateinischen "Peripheria") verwendet hat.
Im Jahre 1767 gelang es Johann Heinrich Lambert (1728 - 1777), aufbauend auf seiner Entwicklung der Funktionen Tangens und Tangens hyperbolicus in Kettenbrüche, zu beweisen, daß π eine irrationale Zahl ist. Somit ist π als unendlicher und nichtperiodischer Dezimalbruch darstellbar. Folglich kann man praktisch niemals mit dem exakten Wert von π rechnen, sondern immer nur mit einem rationalen Näherungswert, etwa π ≈ 3,14 oder genauer π ≈ 3,14159. Auf 30 Dezimalstellen genau lautet dieser Wert:
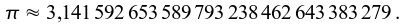
Ebenso ist es mit der Basis e des natürlichen Logarithmus, die als Grenzwert der Zahlenfolge
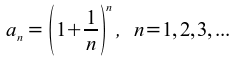
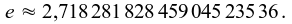
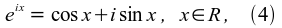
Ohne hier eine ausführliche Einführung der komplexen Zahlen geben zu können, so wollen wir zum Verständnis der Gleichungen (4) und (5) nur kurz Folgendes bemerken: Eine komplexe Zahl z ist ein Ausdruck der Form z := a + bi , wobei a und b reelle Zahlen sind und die imaginäre Einheit i durch i ² = - 1 definiert ist. Für b = 0 ist z = a eine reelle Zahl. Also ist der Bereich R der reellen Zahlen eine Teilmenge des Bereiches C der komplexen Zahlen. Für a = 0 ergibt sich die rein imaginäre Zahl z = bi. Man rechnet mit komplexen Zahlen, grob gesagt, wie mit reellen Zahlen, aber immer unter Beachtung von i ² = - 1. Die Gleichung (4) kann auch als Definitionsgleichung für die komplexe e - Funktion ez mit rein imaginärem Argument z = x i aufgefasst werden.
Zwischen den rationalen und irrationalen Zahlen hatten schon die Mathematiker der Antike unterschieden.
Aber erst seit dem 19. Jahrhundert wird eine weitere Unterscheidung in algebraische und transzendente Zahlen vorgenommen:
Eine reelle (oder komplexe) Zahl a heißt "algebraisch", falls sie Nullstelle eines Polynoms
P(x) = a 0 x n + a 1 x n - 1 + a 2 x n - 2 + ... + a n - 1 x + a n
von mindestens erstem Grade und mit rationalen Koeffizienten a 0 , a 1 , ... , a n
ist. Eine Zahl a, die nicht algebraisch ist, die also keiner algebraischen Gleichung
P(x) = 0 genügt, heißt "transzendent".
So ist z.B. jede rationale Zahl a = p / q (p, q ganz, q > 0) algebraisch, da sie der Gleichung qx - p = 0 genügt. Auch die Irrationalzahl
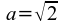ist algebraisch, da sie z.B. der Gleichung x² - 2 = 0 genügt. Und die imäginäre Einheit i ist wegen
ihrer definierenden Gleichung i ² + 1 = 0 ebenfalls eine algebraische Zahl.
Es ist nicht sofort ersichtlich, dass es nichtalgebraische, also transzendente Zahlen gibt.
Der französische Mathematiker Joseph Liouville (1809 - 1882) konstruierte konkrete Klassen transzendenter
Zahlen (Liouvillesche Zahlen) mit Hilfe eines von ihm 1844 bewiesenen Satzes, der beinhaltet, dass sich algebraische Zahlen nicht beliebig gut
durch rationale Zahlen annähern lassen (Liouvillescher Satz über algebraische Zahlen). So zeigte er z. B. die Transzendenz
der Zahl
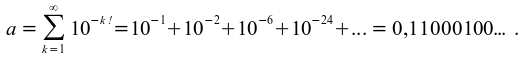
Im Jahre 1873 bewies dann Charles Hermite (1822 - 1901) als erster, dass die Zahl e transzendent ist. Und im Jahre 1882 gelang es schließlich Ferdinand von Lindemann in seiner Arbeit "Die Zahl π" (Mathematische Annalen, 20, 1882), durch eine geniale Übertragung der Hermiteschen Beweismethode die Transzendenz der Zahl π zu beweisen. Er bewies allgemeiner den folgenden "Satz von Lindemann" (auch "Satz von Lindemann-Weierstraß" genannt):
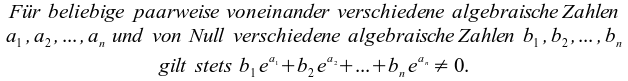
Wir wollen nun kurz den Zusammenhang zwischen der Transzendenz von π und der Unmöglichkeit
der Quadratur des Kreises mit Zirkel und Lineal skizzieren:
Unter einer "Konstruktion mit Zirkel und Lineal" versteht man eine endliche Folge von sog. elementaren Konstruktionsschritten, d. h.
- die Konstruktion der Geraden durch zwei verschiedene Punkte,
- die Konstruktion des Schnittpunktes zweier nichtparalleler Geraden, von denen eine durch zwei verschiedene Punkte gegeben ist,
- die Konstruktion des Kreises um einen gegebenen Punkt durch einen anderen gegebenen Punkt,
- die Konstruktion des Schnittpunktes eines Kreises und einer diesen schneidenden Geraden, wobei der Kreis gegeben und die Gerade durch zwei Punkte gegeben ist
oder die Gerade gegeben und der Kreis durch Mittelpunkt und einen anderen Punkt gegeben ist,
- die Konstruktion der Schnittpunkte zweier sich schneidender Kreise, wobei ein Kreis gegeben und der zweite durch
seinen Mittelpunkt und einen anderen Punkt gegeben ist.
Dabei ermöglicht das "Lineal" das Ziehen einer Geraden durch zwei verschiedene gegebene Punkte
(es muß also keine Maßskala tragen), und der "Zirkel" ermöglicht das Zeichnen von Kreisen
um einen gegebenen Punkt mit Radien, die als Abstände zweier Punkte abgegriffen werden.
Berühmt sind nun die hierauf Bezug nehmenden drei Probleme der klassischen griechischen Mathematik,
nämlich ob es möglich ist, allein mit Zirkel und Lineal
- die Seitenlänge eines Quadrats zu bestimmen, das den gleichen Flächeninhalt wie ein vorgegebener Kreis hat (Quadratur des Kreises),
- die Kantenlänge eines Würfels zu bestimmen, der den doppelten Rauminhalt eines gegebenen Würfels hat (Kubusverdoppelung) bzw.
- einen beliebigen Winkel in drei gleiche Teile zu zerlegen (Winkeldreiteilung).
Mit Hilfe der höheren Algebra, insbesondere der Galoisschen Theorie (Evariste Galois, 1811 - 1832), konnte nachgewiesen werden, dass alle drei
Probleme unlösbar sind. Da aber die höhere Algebra kein Schulstoff ist und im Rahmen dieses Artikels also nicht vorausgesetzt
werden kann, so sei dazu nur folgende stark vereinfachende Umschreibung ausgeführt:
Entscheidend für den Beweis der Unmöglichkeit der Quadratur des Kreises mit Zirkel und
Lineal war der Nachweis der Transzendenz von π durch Ferdinand von Lindemann. Denn
der geometrischen Fragestellung, z.B. eine Strecke aus vorgegebenen
Strecken allein mit Zirkel und Lineal in endlich vielen Schritten zu konstruieren, entspricht
analytisch die Aufgabe, die Länge der gesuchten Strecke mittels rationaler Rechenoperationen
und Quadratwurzeln, d.h. als ineinandergeschachtelte Quadratwurzelausdrücke (durch
Radikale), aus den Längen der vorgegebenen Strecken zu bestimmen. Und bei der Quadratur des Kreises
muss für die zu bestimmende Seitenlänge x des gesuchten Quadrats bei gegebenem Kreisradius r
(r =1 gesetzt) gelten:
x2 = π ⋅ r2 = π bzw.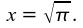
Da aber eine Quadratwurzel bekanntermaßen (als mittlere Proportionale) mit Zirkel und Lineal konstruiert werden kann, so läuft die
Quadratur des Kreises letztendlich darauf hinaus, eine Strecke der Länge &pi aus der Einheitsstrecke zu konstruieren.
Die Länge π lässt sich aber wegen ihrer Transzendenz nicht mittels rationaler Operationen
und Quadratwurzeln aus der Einheitslänge bestimmen, also ist die Quadratur des Kreises allein mit Zirkel und Lineal nicht möglich.
Wir wollen nicht unerwähnt lassen, dass das Problem der Quadratur des Kreises durchaus lösbar
ist, wenn man die Beschränkung des alleinigen Gebrauchs von Zirkel und Lineal fallen läßt,
und auch, wenn man die Euklidische Geometrie verlässt und zur Nichteuklidischen Geometrie übergeht.
Die folgenden beiden Zitate widerspiegeln die Anerkennung, die Ferdinand von Lindemann insbesondere
für den Nachweis der Transzendenz von π und damit der Unmöglichkeit der Quadratur
des Kreises mit Zirkel und Lineal zuteil wurde:
In dem oben schon erwähnten Nachruf "Ferdinand von Lindemann" von C. Carathéodory (Sitzungsberichte der mathematisch-naturwissenschaftlichen Abteilung
der Bayerischen Akademie der Wissenschaften zu München, Jahrgang 1940, S. 61 - 63 ) heißt es:
"Die Entdeckung, welche, solange es noch eine mathematische Wissenschaft geben wird, mit Lindemanns Namen verknüpft sein wird, ist der Beweis der
Unmöglichkeit der Quadratur des Kreises. ... Diese eine Leistung Lindemanns, die einen Glanzpunkt in den mathematischen
Erfolgen der Neuzeit darstellt, überstrahlt alle früheren und späteren Werke unseres verblichenen Kollegen."
Und in den "Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Jahresbericht 1938/39, Seite 75" heißt es:
"Unsterblichen Ruhm hat sich Lindemann durch seinen Beweis für die Transzendenz der Ludolphschen Zahl π erworben. Er
hat damit streng mathematisch bewiesen, daß das uralte Problem der Quadratur des Kreises mit Zirkel und Lineal unlösbar ist. Mit dieser
Großtat menschlichen Geistes wird Lindemanns Name auf alle Zeiten verknüpft bleiben."
Für diejenigen Leser, die sich umfassender für die Geschichte der Mathematik interessieren, seien
z.B. die folgenden drei Bücher genannt:
-Struik, D. J.: Abriss der Geschichte der Mathematik, VEB Deutscher Verlag der Wissenschaften, Berlin 1980.
-Dieudonné, J.: Geschichte der Mathematik 1700 - 1900, VEB Deutscher Verlag der Wissenschaften, Berlin 1985.
-Lexikon bedeutender Mathematiker (Hrsg. S.Gottwald, H.-J.Ilgauds, K.-H.Schlote), Bibliographisches Institut, Leipzig 1990.
Und Leser, die sich mit höherer Algebra, insbesondere der Gruppen-, Ring- und Körpertheorie
sowie speziell mit der Galoistheorie und dem algebraisch exakten Nachweis der Unmöglichkeit der Quadratur des Kreises mit Zirkel und Lineal
beschäftigen möchten, finden in der Buchreihe
-Lugowski, H. / Weinert, H. J.: Grundzüge der Algebra, Teile I (Allgemeine Gruppentheorie), II (Allgemeine Ring- und Körpertheorie)
und III (Auflösungstheorie algebraischer Gleichungen), B.G.Teubner, Leipzig 1968,
eine interessante und gut verständliche Lektüre.